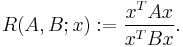Rayleigh quotient
In mathematics, for a given complex Hermitian matrix  and nonzero vector
and nonzero vector  , the Rayleigh quotient[1]
, the Rayleigh quotient[1] 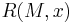 , is defined as[2][3]:
, is defined as[2][3]:
For real matrices and vectors, the condition of being Hermitian reduces to that of being symmetric, and the conjugate transpose 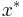 to the usual transpose
to the usual transpose 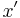 . Note that
. Note that 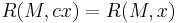 for any real scalar
for any real scalar 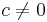 . Recall that a Hermitian (or real symmetric) matrix has real eigenvalues. It can be shown that, for a given matrix, the Rayleigh quotient reaches its minimum value
. Recall that a Hermitian (or real symmetric) matrix has real eigenvalues. It can be shown that, for a given matrix, the Rayleigh quotient reaches its minimum value 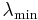 (the smallest eigenvalue of
(the smallest eigenvalue of  ) when
) when  is
is 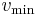 (the corresponding eigenvector). Similarly,
(the corresponding eigenvector). Similarly, 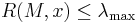 and
and 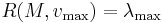 . The Rayleigh quotient is used in min-max theorem to get exact values of all eigenvalues. It is also used in eigenvalue algorithms to obtain an eigenvalue approximation from an eigenvector approximation. Specifically, this is the basis for Rayleigh quotient iteration.
. The Rayleigh quotient is used in min-max theorem to get exact values of all eigenvalues. It is also used in eigenvalue algorithms to obtain an eigenvalue approximation from an eigenvector approximation. Specifically, this is the basis for Rayleigh quotient iteration.
The range of the Rayleigh quotient is called a numerical range.
Contents |
Special case of covariance matrices
A covariance matrix M can be represented as the product 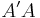 . Its eigenvalues are positive:
. Its eigenvalues are positive:
The eigenvectors are orthogonal to one another:
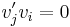 (different eigenvalues, in case of multiplicity, the basis can be orthogonalized).
(different eigenvalues, in case of multiplicity, the basis can be orthogonalized).
The Rayleigh quotient can be expressed as a function of the eigenvalues by decomposing any vector  on the basis of eigenvectors:
on the basis of eigenvectors:
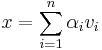 , where
, where 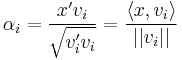 is the coordinate of x orthogonally projected onto
is the coordinate of x orthogonally projected onto 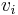
which, by orthogonality of the eigenvectors, becomes:
In the last representation we can see that the Rayleigh quotient is the sum of the squared cosines of the angles formed by the vector x and each eigenvector 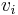 , weighted by corresponding eigenvalues.
, weighted by corresponding eigenvalues.
If a vector  maximizes
maximizes 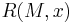 , then any vector
, then any vector 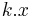 (for
(for 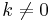 ) also maximizes it, one can reduce to the Lagrange problem of maximizing
) also maximizes it, one can reduce to the Lagrange problem of maximizing 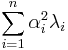 under the constraint that
under the constraint that 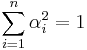 .
.
Since all the eigenvalues are non-negative, the problem is convex and the maximum occurs on the edges of the domain, namely when 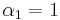 and
and 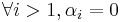 (when the eigenvalues are ordered in decreasing magnitude).
(when the eigenvalues are ordered in decreasing magnitude).
Alternatively, this result can be arrived at by the method of Lagrange multipliers. The problem is to find the critical points of the function
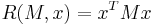 ,
,
subject to the constraint 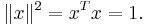 I.e. to find the critical points of
I.e. to find the critical points of
where  is a Lagrange multiplier. The stationary points of
is a Lagrange multiplier. The stationary points of 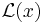 occur at
occur at
and 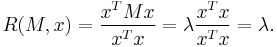
Therefore, the eigenvectors  of M are the critical points of the Raleigh Quotient and their corresponding eigenvalues
of M are the critical points of the Raleigh Quotient and their corresponding eigenvalues  are the stationary values of R.
are the stationary values of R.
This property is the basis for principal components analysis and canonical correlation.
Use in Sturm–Liouville theory
Sturm–Liouville theory concerns the action of the linear operator
on the inner product space defined by
of functions satisfying some specified boundary conditions at a and b. In this case the Rayleigh quotient is
This is sometimes presented in an equivalent form, obtained by separating the integral in the numerator and using integration by parts:
Generalization
For a given pair 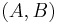 of real symmetric positive-definite matrices, and a given non-zero vector
of real symmetric positive-definite matrices, and a given non-zero vector  , the generalized Rayleigh quotient is defined as:
, the generalized Rayleigh quotient is defined as:
The Generalized Rayleigh Quotient can be reduced to the Rayleigh Quotient 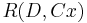 through the transformation
through the transformation 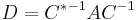 where
where  is the Cholesky decomposition of matrix
is the Cholesky decomposition of matrix  .
.
See also
References
- ^ Also known as the Rayleigh–Ritz ratio; named after Walther Ritz and Lord Rayleigh.
- ^ Horn, R. A. and C. A. Johnson. 1985. Matrix Analysis. Cambridge University Press. pp. 176–180.
- ^ Parlet B. N. The symmetric eigenvalue problem, SIAM, Classics in Applied Mathematics,1998
Further reading
- Shi Yu, Léon-Charles Tranchevent, Bart Moor, Yves Moreau, Kernel-based Data Fusion for Machine Learning: Methods and Applications in Bioinformatics and Text Mining, Ch. 2, Springer, 2011.
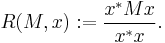
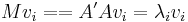
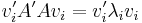
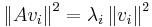
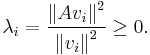
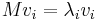
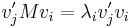
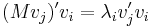
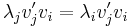
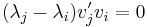
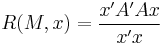
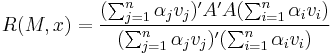
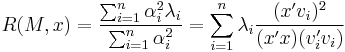
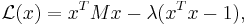
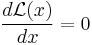
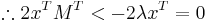
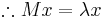
![L(y) = \frac{1}{w(x)}\left(-\frac{d}{dx}\left[p(x)\frac{dy}{dx}\right] %2B q(x)y\right)](/2012-wikipedia_en_all_nopic_01_2012/I/f7a279e06daa340e9ecd72639b512b93.png)
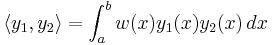
![\frac{\langle{y,Ly}\rangle}{\langle{y,y}\rangle} = \frac{\int_a^b{y(x)\left(-\frac{d}{dx}\left[p(x)\frac{dy}{dx}\right] %2B q(x)y(x)\right)}dx}{\int_a^b{w(x)y(x)^2}dx}.](/2012-wikipedia_en_all_nopic_01_2012/I/ac81866f4aa8cc56e243b677b251644a.png)
![\frac{\langle{y,Ly}\rangle}{\langle{y,y}\rangle} = \frac{\int_a^b{y(x)\left(-\frac{d}{dx}\left[p(x)y'(x)\right]\right)}dx %2B \int_a^b{q(x)y(x)^2} \, dx}{\int_a^b{w(x)y(x)^2} \, dx}](/2012-wikipedia_en_all_nopic_01_2012/I/d8551a06bb0015090df841ba90aa66f5.png)
![= \frac{-y(x)\left[p(x)y'(x)\right]|_a^b %2B \int_a^b{y'(x)\left[p(x)y'(x)\right]} \, dx %2B \int_a^b{q(x)y(x)^2} \, dx}{\int_a^b{w(x)y(x)^2} \, dx}](/2012-wikipedia_en_all_nopic_01_2012/I/e87a1494fc078fcd6c7f6b70047ef17b.png)
![= \frac{-p(x)y(x)y'(x)|_a^b %2B \int_a^b\left[p(x)y'(x)^2 %2B q(x)y(x)^2\right] \, dx}{\int_a^b{w(x)y(x)^2} \, dx}.](/2012-wikipedia_en_all_nopic_01_2012/I/7128e347e30563e26611a9b199108f2c.png)